Section: Scientific Foundations

Modelling of Multiphase Media

Conventional one-dimensional models of two-phase mixtures having two velocities form a system of six partial differential equations: two mass, two momentum and two energy equations. Those models are not hyperbolic and are consequently ill posed. It means that there is no continuous dependance from initial data and boundary conditions to the solution. In other words, wave propagation may have no physical sense.

This issue has been understood by [47] and subtle remedy was given by [23] . They proposed an extended model with seven equations. The extra differential equation replaced the pressure equilibrium assumption in the mixture. Thanks to this new equation, the model was correctly posed, unconditionally hyperbolic.

This model had little diffusion as it was presented in the context of a specific problem of detonation physics. Also, the model was difficult to solve at the numerical level, in particular with modern algorithms based on the Riemann problem solution. In [42] we developed the first Godunov type method for this model and derived accurate approximation formulas for the non-conservative terms. Moreover, a specific relaxation method was built in order to solve these equations in the presence of stiff relaxation terms. This issue was particularly important as,

• this model was involving two pressure and two velocities,

• at an interface the jump condition corresponds to continuous normal velocities and continuous pressures,

• in order to fulfill this condition it was necessary to relax the two pressures and velocities to unique equilibrium variables.

Such an issue was reached by using specific relaxation solvers, with infinite relaxation parameters like in [5] . With this solver, the model was able to solve interface problems (air/water for example) and multiphase mixtures with two velocities. Important applications of fundamental and applied physics were possible to solve. Financial supports from DGA and CEA helped us to pursue the investigations.

Denoting $p_r=p_1-p_2$, $u_r=u_1-u_2$, the two-phase flow model presents under the form (1 ) :

Only the equations for phase 1 are written, since those of phase 2 are symmetric. General closure relations for this system need the determination of :

• the interface velocity $u_I$ and pressure $p_I$ that respectively represent the velocity and pressure that exert at the boundary of a cloud of bubbles or droplets,

• the average interface velocity $u_I^{{}^{\text{'}}}$ and pressure $p_I^{{}^{\text{'}}}$ that exert in the bulk of a two-phase control volume,

• the relaxation parameters $\lambda$ and $\mu$ that control the rate at which velocities and pressures relax to mechanical equilibrium respectively.

These relations were unknown, either estimated in limit cases only, or determined by experimental means. In order to determine these closure relations a new homogenization method has been built in [1] .

This new averaging method considers the mixture at the discrete level, with a stencil composed of three computational cells. In each cell, at each cell boundary and at each internal boundary separating the phases, the Riemann problem of the pure fluid equations (RP) is solved. The RP solution provides all local interfacial information. These RP solutions are then averaged in the computational cell as done originally with the first version of the Godunov method, derived originally for the Euler equations. In our context, extra difficulties appear, due to the presence of internal material interfaces, material discontinuities at cell boundaries and variable sub-volumes, due to the phase presence in the cells. But the philosophy was the same as with the Godunov method : we are dealing with average RP solutions and not with discretized partial differential equations.

The resulting system of this averaging procedure is a quite complicated discrete system in algebraic form. It corresponds to the result of the Discrete Equations Method (DEM). The closure relations for the various interface variables have been obtained by reaching the continuous limit of these discrete equations [8] , [24] that provide information easier to interprete than discrete formulas.

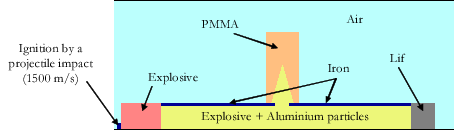
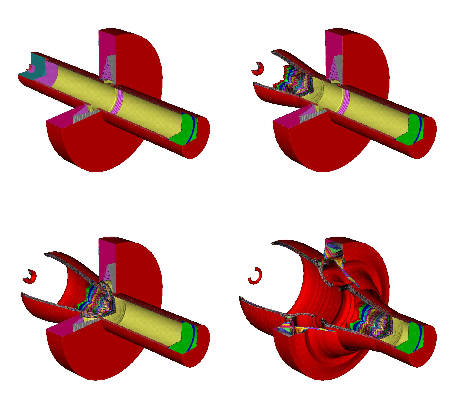
With this strong modelling foundations, it was possible to consider problems with extended physics : turbulence, phase transition, ions and electrons in plasma mixtures, granular materials, chemical reactions, continuum media with elastic-plastic effects. An example is shown in the figures 2 -3 .

Figure 2. A steel tube is filled with a heterogeneous explosive. A high velocity impactor creates a shock wave passed onto the explosive, that becomes a detonation wave.

Figure 3. After a short period of time the shock wave becomes a detonation wave that produces gas and solid products at very high pressure. They set into intense motion solid tube walls. Two different types of mixture are present in this type of application : a physical one, corresponding to the mixture of gases and solid particles during the detonation dynamics, and artificial mixtures, corresponding to the ones that appear at material interfaces, here at the gas - steel tube boundary. Both types of mixture are solved by the same equations and the same numerical algorithm [43] . Moreover, the detonation dynamics is checked against generalized CJ solutions [41] , specifically determined for this temperature non-equilibrium model.

Most of these extensions are done with the help of the Hamilton principle of least action [46] , [3] to develop appropriate single phase material models that are then coupled with the DEM to form a multiphase flow model.